Matematika v biológii
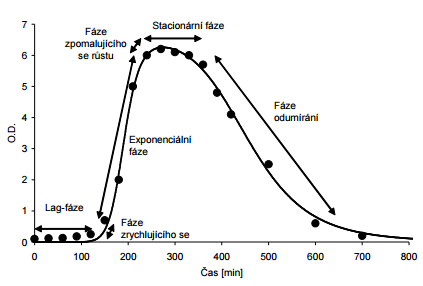
♠ V exponenciálnej fáze rastu mikroorganizmov (viď obrázok vpravo) sa dá vysledovať niekoľko dôležitých matematických vzťahov, ktoré slúžia k charakterizácii danej populácie a napr. k biotechnologickým výpočtom.
♠ V exponenciálnej fáze rastu se bunky delia geometrickým radom, úmrtnosť je zanedbateľná. Po uplynutí generačnej doby sa populácia zdvojnásobí.
♠ Označíme si množstvo buniek symbolom N (v akýchkoľvek vhodných jednotkách, napr. počet organizmov), počiatočné množstvo buniek na začiatku exponenciálnej fáze N0 a generačnú dobu g. Potom sa dá množstvo buniek po uplynutí času t vyjadriť ako:
N = N0 . 2t/g | Ak nasadíme mikrobiálnu kultúru do nového životného prostredia a budeme sledovať množstvo
mikroorganizmov v závislosti na čase, získame tzv. rastovú krivku. Tá má obyčajne tvar vyobrazený na
obrázku:
 |
| Úloha č. 1.a): Do vhodného prostredia sme umiestnili 1024 baktérií, ktorých generačná doba je 24 minút. Koľko baktérií bude v tejto populácii po dvoch hodinách, ak vieme, že sa nachádzajú v svojej exponenciálnej fáze? | . Baktérií bude . |
| Úloha č. 1.b): V predchádzajúcej situácii vypočítajte, koľko baktérií pribudne k pôvodnému počtu za 12 minút, ak vieme, že generačná doba trvá 24 minút. | Bude ich tam približne , takže pribudne baktérií. |
| Úloha č. 1.c): Za aký čas sa z 1024 baktérií vo svojej exponenciálnej fáze vytvorí populácia s 8 násobným množstvom baktérií? | Bude to trvať minút. |
| Úloha č. 2): Za aký čas sa z istého množstva baktérií vo svojej exponenciálnej fáze vytvorí populácia s 32 násobným množstvom baktérií, ak ich generačná doba je pol hodiny? | Bude to trvať minút. |
| Úloha č. 3: Bacillus subtilis je baktéria žijúca v pôde. Aká je jej generačná doba, ak sme v exponenciálnej fáze rastu pozorovali, že populácia 100 baktérií Bacillus subtilis po uplynutí 129 minút narástla na 3200 baktérií? | Generačná doba baktérie Bacillus subtilis je minúty. |
Úloha č. 4: Zistite, ktorá z baktérií má dlhšiu generačnú dobu, ak sme pozorovaním počas expozičnej fáze zistili tieto skutočnosti:
A (Mycobacterium tuberculosis): populácia 500 baktérií sa za 12 hodín zdvojnásobila.
B (Saccharomyces cerevisiae): populácia 100 baktérií narástla na 1600 za 8 hodín. | Dlšiu generačnú dobu má: - uveďte iba písmeno |
Úloha č. 5: Po uplyntí akého času budeme mať v dvoch miskách A, B s rôznymi baktériami rovnakopočetnú populáciu, ak na začiatku merania sme zistili takéto počty baktérií:
A: Streptococcus thermophilus (generečná doba 0,20 hod) v počte 120 kusov
B: Escherichia coli (generačná doba 0,35 hod) v počte 240 kusov | Rovnaké množstvo baktérií v týchto miskách bude po uplynutí času minút. |