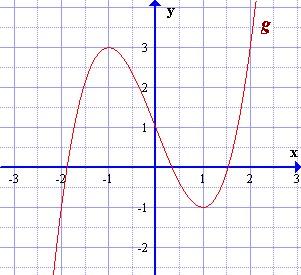
 | Na obrázku vľavo je znázornený graf funkcie g. Z grafu urč tieto funkčné hodnoty:
g(0) = ; g(-1) = ;g(1) = ; g(-2) = ; g(2) =
Zapíš všetky x, pre ktoré je g(x) = 3 (začni najmenším): ;
Nájdi všetky x, pre ktoré je g(x) = -1 (začni najmenším): ;
Priesečník s osou y má súradnice Py [; ]
Funkcia g má takýto počet koreňov (tzn. g(x)=0): |
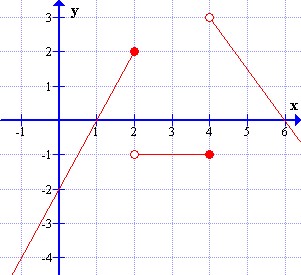 | Z grafu nespojitej funkcie f na obrázku vľavo urč:
funkčná hodnota v bode 1 je
funkcia nadobúda v bode 4 hodnotu
funkčnú hodnotu -4 nadobúda funkcia f v bode
funkcia f nadobúda v bode 0 hodnotu
f(3) =
funkcia f má 2 korene (začni najmenším): ;
priesečníky s osou x sú: Px1 [; ], Px2 [; ]
priesečník s osou y má súradnice Py [; ] |
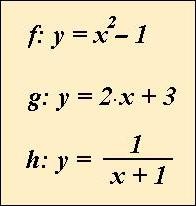 | Vľavo sú dané predpisom tri funkcie f, g, h. Zisti:
f(-2) = ; f(2) = ; f(-1) = ; f(1) =
zapíš, pre aké x je funkčná hodnota f(x) = 8 (začni najmenším): ;
nájdi korene funkcie f (tzn. kde pretína graf x-ovú os): x1 = ; x2 =
funkčná hodnota funkcie f v bode 0 je
g(1/2) =
graf funkcie g pretína y-ovú os v bode so súradnicami [0; ]
g() = 7
funkčná hodnota funkcie g v bode je 1
funkcia h nadobúda v bode x = 0 hodnotu
h(2) =
funkčnú hodnotu -1 nadobúda funkcia h v bode x =
h() = 1 |